Uncertainty Quantification Toolkit
Overview
The Uncertainty Quantification Toolkit (UQTk) is a lightweight open source C++ library, (available at http://www.sandia.gov/UQToolkit) primarily offering tools for the propagation of uncertain inputs and parameters through a computational model.
UQTk allows other researchers to apply our algorithm UQ research to many other applications. It is well suited for algorithm prototyping, as well as for educational and tutorial purposes.
UQTk counted 600 downloads as of April 2016, for these and other common uses:
- Key research code for UQ group at Sandia’s CRF
- Part of QUEST SciDAC institute: http://www.quest-scidac.org
- Part of many research collaborations in the US DOE SciDAC program
- Use in DOE BER ACME climate model postprocessing
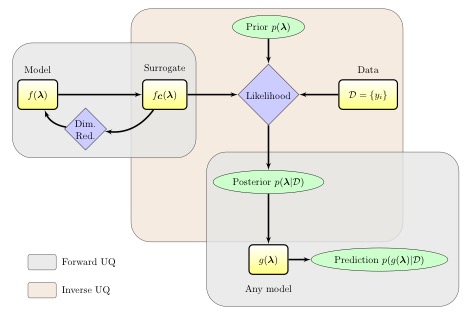
Figure 1 UQTk can be used to create comprehensive and application-specific workflows for calibration, sensitivity analysis, and forward uncertainty quantification (UQ).
Key Contributions
- UQ in LES predictions: Provided with stated uncertainties in LES subgrid model parameters, we demonstrated forward UQ in LES computations of turbulent combustion. Results highlight the different ways in which each uncertain parameter impacts uncertainty in predictions
- UQ for LES model inputs: We estimated uncertainty in parameters of a chemical model used as an input to LES of turbulent combustion. This study highlighted the utility of accounting for model error in chemical model calibration for subsequent use in predictive simulations
Technical Details
UQTk provides the following features:
- Functionalities to enable intrusive UQ, in which uncertain variables are represented with spectral polynomial chaos (PC) expansions. Intrusive functionalities include routines for evaluating algebraic expressions and transcendental functions of random variables [1]
- Functionalities for non-intrusive UQ, including quadrature-based spectral projection methods
- Regression-based approaches, such as polynomial regression, radial basis function, and Gaussian process regression
- Libraries for solving inverse problems via Bayesian inference, including a variety of methods for Markov chain Monte Carlo (MCMC)
The full list of methods, examples and utilities are described in the UQTk manual [2]. Also, “The Uncertainty Quantification Toolkit” chapter in [3] provides an example workflow with a range of UQTk functionalities illustrated.
- Bert Debusschere
- Khachik Sargsyan
[1] B. Debusschere, H. Najm, P. Pébay, O. Knio, R. Ghanem and O. Le Maître (2004). “Numerical challenges in the use of polynomial chaos representations for stochastic processes”. SIAM journal on scientific computing, 26(2), 698-719
[2] B. Debusschere, K. Sargsyan and C. Safta (2013). “UQTk Version 2.1 User Manual”
[3] B. Debusschere, K. Sargsyan, C. Safta, and K. Chowdhary (2016). “The Uncertainty Quantification Toolkit (UQTk)”, to appear in “Handbook of Uncertainty Quantification”, R. Ghanem, D. Higdon, H. Owhadi (Eds), Springer, ISBN 978-3-319-12386-8 (due out May 8, 2016)