Stochastic models are useful in chemical modeling at intermediate scales. Our work in this area includes the development of numerical methods for dealing with stiffness in the chemical Langevin equation and in kinetic Monte Carlo models.
Stiffness in Stochastic Chemical Models
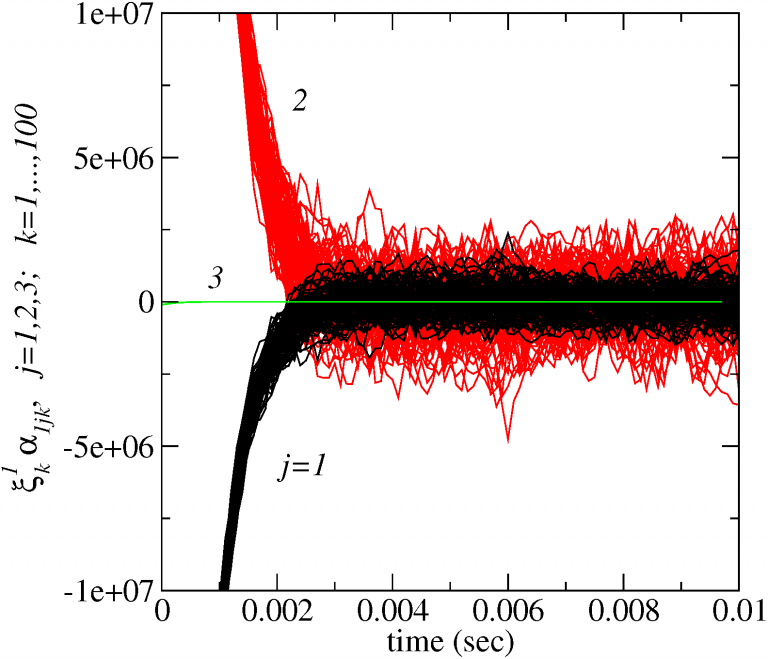
We have developed time integration strategies that target efficient handling of large ranges of time scales in stochastic computational models of mesoscale chemical systems, focusing specifically on the chemical Langevin equation (CLE), a stochastic differential equation. We developed methods relying on computational singular perturbation (CSP) analysis for dealing with stiffness in the CLE drift terms, and on alternate localized linearization strategies for modeling fast CLE diffusion processes. The combination of both approaches can enable large time-step explicit time-integration of stiff CLE systems. We are extending and developing these methods to handle discrete stochastic models encountered in kinetic Monte Carlo (KMC) modeling of surface kinetics, where, again, stiffness can be a major hurdle for time integration of these systems over long time horizons.
POC: Habib N. Najm