We develop data science and machine learning (ML) methods targeted at advancing the state of the art in the computational modeling and analysis of physical systems. We focus particularly on scientific ML, where ML systems are constrained by available physical laws, aside from the explicit learning from data.
Machine Learning for Hydrocarbon Clustering
Together, the availability of high-throughput data generation tools, extensive access to high-end computational hardware, and recent developments in ML methods and tools have enabled a revolution in computational studies of chemical systems. We are working on the use of automated chemical exploration tools and ML for enabling the investigation of reaction processes in heavy hydrocarbons. We use neural network (NN) models, relying on physics-constrained feature vector representations, to represent potential energy surfaces (PESs) of a class of heavy hydrocarbon molecules. We use KinBot for exploration of molecular geometries, and ab initio quantum chemistry computations at select points, to provide data for training and testing NN PES constructions. We construct and use databases that include computed energies and forces for molecular structures that span reaction pathways, saddle point regions, and PES basins. We use the resulting trained NN PES for computation of reaction rates. We also develop effective and efficient strategies by employing active learning, force training, and multilevel multifidelity NN constructions to facilitate NN training with minimal number of samples. Our NN training tools rely on open source Python PyTorch ML capabilities and use GPU hardware on both local computational servers and DOE supercomputing facilities. (PIs: Habib Najm, Judit Zádor, and Mike Eldred)
Physics-Informed NNs for E3SM Land Model
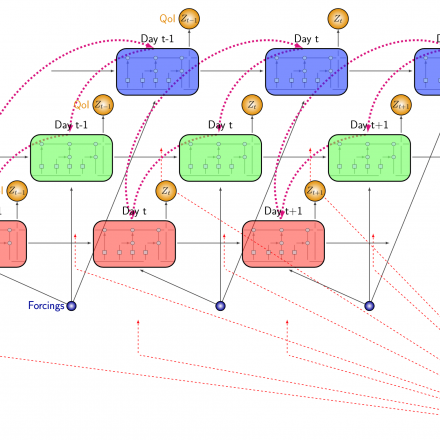
In collaboration with climate modelers from several national laboratories, we develop predictability and uncertainty quantification methods for the land component of the DOE flagship climate model, Energy Exascale Earth System Model (E3SM, www.e3sm.org). We construct surrogate approximations for the E3SM Land Model (ELM), which captures a wide range of processes, including photosynthesis and biogeochemistry. Due to the temporal nature of the model, we construct a surrogate with a recurrent neural network (RNN) architecture with long-short term memory (LSTM) units. We then augment the architecture with a hierarchical structure of the relationships between the various inputs, state variables, and output quantities of interest (QoIs). The resulting hierarchical LSTM RNN mimics the physical constraints and relationships between the underlying processes and provides a natural structure for temporal evolution. (PIs: Khachik Sargsyan, Cosmin Safta)
Figure 1 Demonstration of the specialized LSTM architecture that includes customized connections between QoIs that are related to each other in the E3SM land model.
Neural ODEs
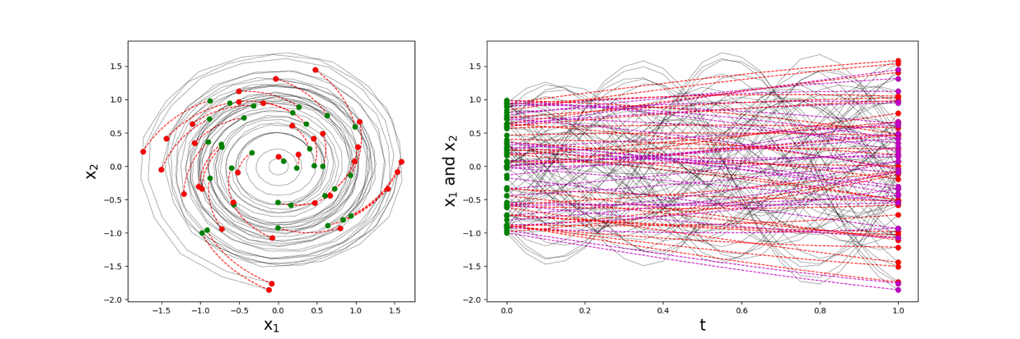
We develop both a rigorous framework and mathematical analysis tools for Residual Networks (ResNets), a broad class of NNs. The work focuses on neural ordinary differential equations (ODEs), an NN formulation viewed as a continuous limit of ResNets as the number of hidden layers approaches infinity. We augment NNs with probabilistic weights and exploit the analogy between ODE evolution and NN forward prediction through layers. This joint viewpoint opens unprecedented opportunities for analyzing NNs as random dynamical systems using established tools from computational singular perturbation, stability analysis, and uncertainty quantification. Exploiting NN/ODE model reduction or imposing structural restrictions on associated ODEs leads to well-grounded non-heuristic means for regularization improving NN generalization and predictive skills, particularly in regimes with scarce and noisy data. This work has a potential impact on ML systems used in materials science and earth system modeling. (PIs: Khachik Sargsyan, Marta D’Elia, and Habib Najm)
Figure 2 Two-dimensional linear ODE learning of the map from initial conditions (input) to final result (output). The learning mechanism implicitly regularizes and finds the shortest path to the output.
Bayesian ML
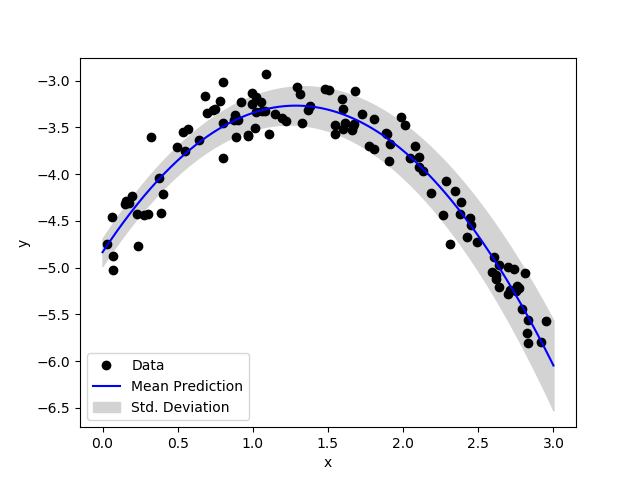
Probabilistic approaches to ML, particularly NNs, provide the necessary regularization of the typically overparameterized NNs while leading to predictions with uncertainty that are robust with respect to the amount and quality of input data, including adversarial scenarios. Bayesian probabilistic modeling, which is recognized as the main machinery behind probabilistic ML approaches, provides a coherent framework for reasoning about ML predictive uncertainties. We explore both sampling-based (various flavors of Markov chain Monte-Carlo) and approximation-driven methods (Approximate Bayesian Computation and variational inference) toward Bayesian NN in which typically deterministic NN weights and biases are endowed with parameterized probabilistic structure. Resulting uncertainty estimation in ML predictions allows construction of noise models for physical model calibrations, optimal experimental design, and active learning further down the model development pipeline. (PIs: Khachik Sargsyan, Habib Najm)
Figure 3 Demonstration of an example problem: Bayesian training of a polynomial-layer neural network via variational inference, given noisy data.