Our work in uncertainty quantification (UQ) includes a range of research activities having to do with the quantification of uncertainty in computational model inputs and outputs. The work involves a focus on the development of numerical methods and open source software for statistical learning from data, forward propagation of uncertainty in computational models, and model selection/validation. We work on addressing major challenges in this area, including the large number of parameters typically encountered in physical system models, and the large computational cost of high-fidelity of numerical computations of relevant physical systems. We provide tools based on our UQ developments in the open-source computational UQ toolkit UQTk.
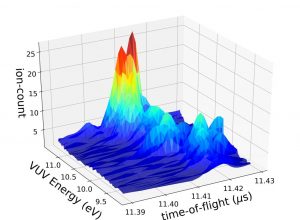
Figure 1 Shown is the calibrated model prediction with a model error correction for one of the peaks in the time-of-flight spectrum. Including model error enables the predictive model to capture complex yet unmodeled physics, e.g., the position of the maximum ion-count varying with energy.
Optimal Experimental Design
Our work in optimal experimental design (OED) focuses on developing capabilities for Bayesian OED in reacting flow experiments, with an application in the design of time of flight mass spectroscopy measurements in a high-pressure photolysis experiment. We rely on a Bayesian calibrated instrument model to provide predictions of the experimental response with requisite handling of parametric uncertainty and model error. This model forms the kernel underlying the Bayesian OED process. We compute an optimal design by maximizing the expected information gain for a parameter of interest. In high-dimensional models, this can become computationally prohibitive. We are developing methods that efficiently compute and optimize the expected information gain over a constrained design space. We work on tailoring the OED framework to meet the goal of a particular project, e.g., by targeting a selection of reaction rate parameters. Experimental measurements at the identified optimal design will be used to improve our knowledge of the reaction rate parameters, and of the underlying Bayesian-calibrated model, and to help validate the overall OED strategy. (PIs: Habib Najm, Leonid Sheps)
UQ in Discrete Systems
While most random variables in physical systems are continuous in nature, discretely valued variables show up in many areas. For example, in the field of cyber security, random variables such as the number of infected nodes, the amount of CPUs per node, or the nominal network bandwidth are all discrete. In this work, we employ Polynomial Chaos Expansions (PCEs) that have been tailored to discrete random variables and their probability masses, to build functional representations of a given Quantity of Interest with respect to those discrete random variables. This allows us to assess the uncertainty in the Quantity of Interest, as well as how sensitive it is with respect to each of the inputs. These tools have been implemented in PyApprox (https://github.com/sandialabs/pyapprox) in the context of the Sandia SECURE Grand Challenge LDRD project. (Bert Debusschere, Laura Swiler, Gianluca Geraci, John Jakeman).
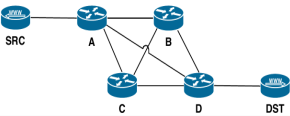
Figure 2 Sensitivity analysis of the number of requests per second that a webserver can fulfill, in a situation with 4 routers between the client and the server. The number of requests fulfilled is most sensitive to the network parameters on the path SRC – A – D – DST, and least sensitive to the link B – C.
Model Error
The calibration of computational models of physical systems typically assumes that the computational model replicates the exact mechanism behind data generation. As a result, calibrated model parameters are often biased, leading to deficient predictive skills. We developed a Bayesian inference framework for representing, quantifying, and propagating uncertainties due to model structural errors by embedding stochastic correction terms in the model. The embedded correction approach ensures physical constraints are satisfied, and renders calibrated model predictions meaningful and robust with respect to structural errors over multiple, even unobservable, quantities of interest. The physical inputs and correction parameters are simultaneously inferred via surrogate-enabled Markov chain Monte Carlo. With a polynomial chaos characterization of the correction term, the approach allows efficient decomposition of uncertainty that includes contributions from data noise, parameter posterior uncertainty, and model error. The developed structural error quantification workflow is implemented in the UQ Toolkit (https://www.sandia.gov/uqtoolkit). We work on applying this method in a range of practical applications of DOE interest from fusion science to fluid dynamics to climate land models [https://doi.org/10.1615/Int.J.UncertaintyQuantification.2019027384]. (Khachik Sargsyan, Habib Najm)
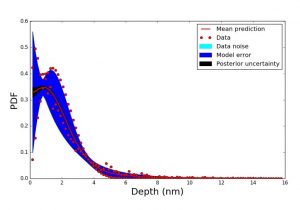
Figure 3 Embedded model-error accurately captures discrepancies and becomes part of uncertainty decomposition in prediction of tungsten depth probability density function. Application in computational study of tungsten wall material damage under fusion plasma conditions. [10.1615/Int.J.UncertaintyQuantification.2018025120]
Global Sensitivity Analysis & UQ in Large-Scale Computational Models
UQ in large-scale computational physics models is highly challenging given the typically large number of uncertain parameters, and hence the high dimensionality of the input space requiring exploration, coupled with the large per-sample computational cost. Global sensitivity analysis (GSA), targeting the identification of dominant uncertain model inputs, is a key element of a scalable UQ strategy. Distinct from local sensitivity information provided by differential methods built on gradient information, GSA provides valuable sensitivity information across a range of parameter values (i.e. non-local) including capturing critical joint-interaction effects between parameters. We have developed and used an efficient GSA/UQ workflow, making use of polynomial chaos methods employing sparse quadrature enabled projection techniques and sparsity promoting regularized regression approaches to provide typically orders of magnitude reduction in the computational costs for a given accuracy requirement by leveraging the intrinsic smoothness and low-dimensional structure exhibited in physical models. We have demonstrated this construction in materials modeling in fusion and fission energy applications, showing the drastic decrease in effective uncertain parameter dimension once GSA information is considered. [https://doi.org/10.1137/17M1141096](Tiernan Casey, Khachik Sargsyan, Habib Najm)
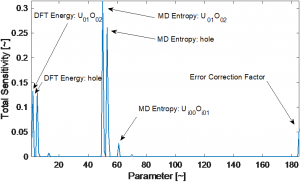
Figure 4 Total sensitivity indices for model inputs from GSA of diffusivity predictions from a cluster dynamics model for transport in uranium fuel. GSA reveals that only on the order of 10 parameters from an input set of more than 180 are influential on prediction variance.
POC: Habib N. Najm