Habib Najm, Khachik Sargsyan, and Bert Debusschere of the CRF, working with Cosmin Safta of Sandia’s Computer Sciences and Information Systems center and Robert Berry, formerly at the CRF and presently at The Climate Corporation in San Francisco, California, have demonstrated the use of a data free inference (DFI) approach [1] for uncertainty quantification (UQ) in reacting flow computations.
In general, predictive computations of reacting flow should provide an estimation of uncertainty in model outputs. This, in turn, requires estimates of uncertainty in models and their parameters. This uncertainty is rooted in several sources, such as the requisite choice of species and reactions defining the chemical kinetic mechanism structure, as well as the values of chemical model parameters, including both thermodynamic and chemical kinetic rate parameters.
In particular, chemical reaction rates are typically modeled using Arrhenius expressions. Each of these involves a baseline of three parameters: the pre-exponential constant A, temperature exponent n, and activation energy E. These parameters—commonly estimated from experimental measurements, ab-initio computations, or rate rules—exhibit a degree of uncertainty.
UQ methods can be used to propagate chemical kinetic rate parameter uncertainties forward through reacting flow computations to generate estimates of uncertainty in model predictions. In solving this forward UQ problem, using a probabilistic formulation to represent uncertainty is the best way to adequately deal with large uncertainty and model nonlinearity. This context requires a full probabilistic characterization of the uncertain input space, through, for example, a joint probability density function (PDF) on the uncertain parameters.
Such PDFs are, however, typically not available in the chemical kinetics literature. At best, the literature provides nominal values and error-bars on A, only nominal values of (n, E), and no information on the correlation structure among the three parameters. Yet these parameters are clearly correlated via the procedure used to estimate them. Assuming them to be simply independent is unacceptable, because this can result in the assignment of significant probability to parameter values that do not fit the data and are inconsistent with the physics.
Also generally unavailable is the original data used to estimate the parameters. If this data were available, one could arrive at the requisite joint PDF by redoing the fitting using statistical inference methods. In the absence of the original data, UQ in reacting flow computations presents the challenge of constructing a joint PDF on uncertain model parameters that is consistent with whatever information is available.
The DFI approach explored in this work—which is based on a maximum entropy formulation on the joint data-parametric space—seeks to discover a joint PDF for the data-parameter space that satisfies given constraints. It relies on a random walk procedure on the data space, proposing data sets and retaining those that are consistent with the given information. The data consistency check involves the use of Bayes’ rule to estimate a posterior PDF on model parameters, whose statistics are compared to the given constraints. Posterior PDFs available from consistent data sets are averaged (or “pooled”), yielding the pooled DFI posterior density.
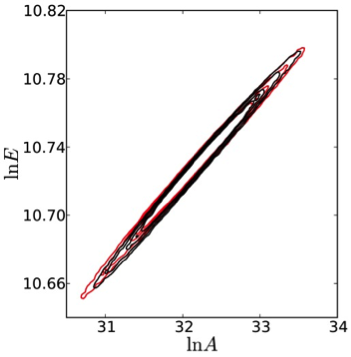
The team demonstrated the method on homogeneous ignition of a stoichiometric methane-air mixture at atmospheric pressure over a range of initial temperatures. Using synthetic noisy data for ignition time dependence on initial temperature, the researchers employed Bayesian inference to establish a joint posterior PDF on (ln A, ln E) parameters of a single-step global methane-air kinetic model. Simulating a typical experimental-fitting scenario, this PDF was discarded after retaining select statistics, namely nominals and marginal bounds. DFI was used to discover a joint PDF on the two parameters that would be consistent with available information—namely the nominals/bounds, the range of initial temperature of the synthetic “experiment,” the global methane-air model used for fitting, and the data noise structure—in the absence of the original data.

Notably, the study illustrated the strong correlation between the kinetic rate parameters evident in the reference posterior PDF obtained from the Bayesian inference procedure. Further, results highlighted the effectiveness of the DFI procedure in generating data sets that are clustered in the vicinity of the missing data. Moreover, the consistent posteriors were found to exhibit very similar structure to the baseline density, with only minor variations between the structures of each. Consistently, the pooled DFI posterior, based on 175,000 consistent data sets, was very close to the baseline density, as shown in Figure 1. This remarkable agreement is not necessarily expected, and may be less notable in other contexts, depending on the available information on the system at hand. The agreement suggests that the available information in this case is very nearly a sufficient statistic, encapsulating most of the information in the missing data.
This encouraging performance motivates the extension of the method to more realistic situations. Work in progress will assess the performance of the algorithm, given bounds on a subset of the parameters, such as only A. In addition, the method will be applied for the construction of the uncertain input space of an elementary-step kinetic mechanism. Initial testing will target a hydrogen-oxygen mechanism, and will involve cataloguing of available information from the literature on each of the reactions. In this context, correlations among parameters of each reaction, as well as among those from different reactions, are expected, depending on the fitting models employed. Construction of the joint PDF on the full set of parameters of this hydrogen-oxygen model will enable meaningful and reliable estimation of uncertainty in associated reacting flow predictions.
[1] Habib N. Najm, Robert D. Berry, Cosmin Safta, Khachik Sargsyan, and Bert J. Debusschere, “Data Free Inference of Uncertain Parameters in Chemical Models,” International Journal for Uncertainty Quantification, in press.