Seeking to free researchers from a nearly exclusive dependence on empirical models, CRF researcher Ahren Jasper and Argonne National Laboratory researchers James A. Miller and Stephen J. Klippenstein have developed a set of theoretical methods for predicting the rates of collisional energy transfer that govern pressure dependence.1 Enabled by both the increased availability of high-performance computing resources and advances in the theoretical understanding of energy transfer, this work helps complete a set of theoretical methods for characterizing elementary chemical reactions in combustion entirely from first principles.
Background
The difficulty in creating a comprehensive set of first-principles theoretical methods for combustion lies in the complexity of many typical combustion reactions. Textbook chemical reaction representations (e.g., A + B → C + D) suggest that reactants are converted directly to products. However, many elementary reactions are not so simple. Instead, reactants can combine to form transient, energized intermediates (A + B → I*), which may be connected by chemical rearrangements to other intermediates (A +B→I1*→I2* → …). Each energized intermediate, in turn, may fragment to different sets of bimolecular products.
Adding further complication, fragmentation pathways generally compete with collisional stabilization pathways, such as those responsible for molecular growth
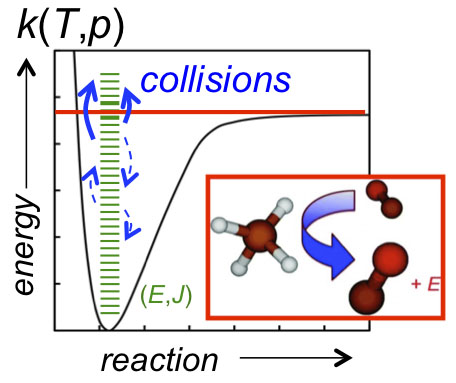
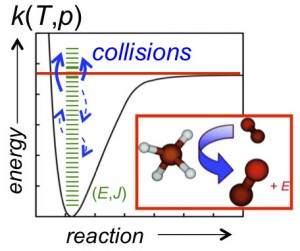
(A + B → I* (+ M) → I (+ M)). Collisional stabilization—and activation in unimolecular reactions (A (+ M) → A* (+ M) → B + C)—gives rise to pressure dependence in chemical reactions (as illustrated in Figure 1), and the probabilities of forming the various competing products can be a sensitive function of both temperature and pressure. Predicting chemical-reaction outcomes over the broad temperature and pressure ranges common in combustion applications requires knowing the microscopic rates of the various competing pathways.
Theoretical Predictions of Microscopic Rates
Since its formulation in the 1930s, transition state theory has been refined into a quantitative, first-principles method for calculating microscopic rates for myriad processes involving bond breaking or bond forming. Developing first-principles methods for predicting collisional energy transfer rates, on the other hand, has been largely neglected. The new methods developed by the CRF-Argonne team fill this gap.
The competition between chemical pathways (bond breaking and forming) and collisional energy transfer pathways (stabilization and activation) is theoretically characterized by a master equation (ME) that tracks the coupled time-dependence of the various microscopic (E,J-resolved) reactant, product, and intermediate populations. E and J are state labels that describe the chemical species’ total energy and total angular momentum, respectively.
The ME terms that account for energy transfer include the collisional state-to-state rate coefficient, kc,i(E,J ← E’,J’), which is proportional to the rate at which collisions knock the ithchemical species from some initial internal state (E’,J’) to some other state (E,J), as shown in Figure 1. The state-to-state rate coefficient can be written as the product of the total collision rate, Z, and the normalized probability, Pi(E,J ← E’,J’), of a collision producing the state (E,J) from an initial state (E’,J’).
Rather than characterize the four-dimensional function Pi in detail, the team instead characterized Pi in terms of low-order moments of the change in E and J due to collisions. While the emphasis on low-order moments may miss fine details of Pi, the overall kinetics is expected to depend most sensitively on only the first few moments. Further, the calculated kinetics can be systematically converged by including higher and higher-level moments.
The moments themselves may be accurately calculated using classical mechanics and ab initio potential energy surfaces. The use of classical mechanics is motivated by the Ehrenfest theorem, which states that averaged quantum mechanical variables (nearly) obey classical laws, and the knowledge that the high internal energies of combustion applications wash out quantum effects as the classical (high-E) limit is approached.
To minimize a more likely source of significant error—the description of the potential-energy surface that governs the collisions—the research team used so-called “direct dynamics.” Avoiding the usual step of fitting analytic (but usually approximate) potential-energy surface representations in their direct dynamics calculations, the researchers instead coupled the trajectory code with quantum chemistry codes and directly calculated the potential-energy surface when needed. This computationally demanding work benefits from the CRF’s high-performance computing resources, as well as Department of Energy (DOE) resources at the National Energy Research Scientific Computing Center (NERSC).
The reformulated ME provides a crucial advantage: allowing useful convergence of the low-order moments by running only hundreds of trajectories—rather than the millions of trajectories needed to characterize the full four-dimensional function Pi. Thus, this approach provides a generally applicable and efficient means of predicting energy transfer rates without empiricism.
Validation Confirms Value in More Complex Systems
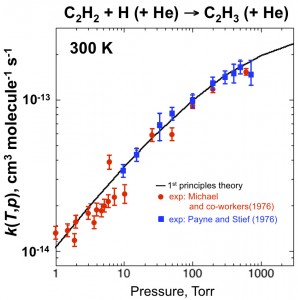
The team validated this first-principles approach, along with high-level transition-state theory and thermochemistry calculations, against experimental data on pressure-dependent kinetics for several simple unimolecular dissociation reactions. As depicted in Figure 2, the parameter-free theory agrees quantitatively with two sets of experimental results. These validations confirm that the approach presented here enables quantitative rate determinations and supports its application to more complex systems where experimental information is often not available. Overall, this work greatly expands the variety of chemical reactions that can be studied quantitatively and entirely from first principles.